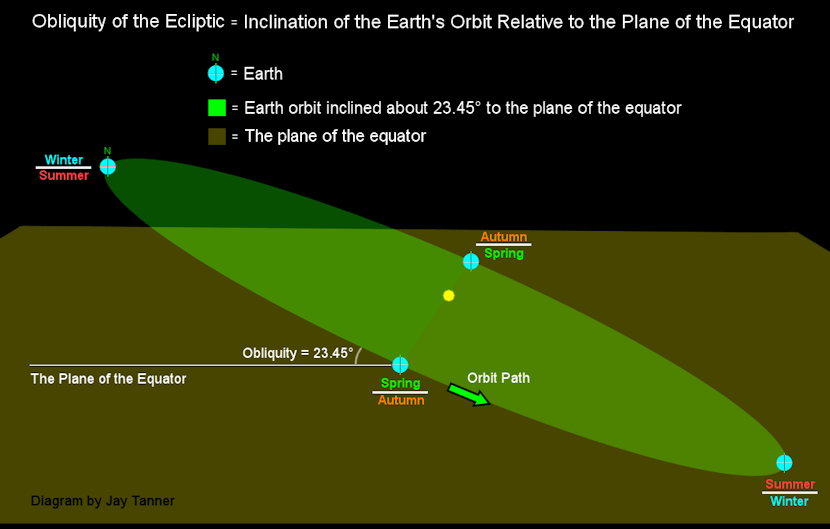
The obliquity of the ecliptic is essentially the angle of inclination of the Earth's orbit with respect to the plane of the equator, which to us, produces the apparent relative tilt of the Earth's polar axis which is the principal cause of the annual seasons. Even though the Earth's moves in an inclined orbit, the north pole is remains upward, as in the diagram above.
This angle is approximately ±23.45 degrees and is the apparent maximum/minimum angle of the sun above or below the equator during the year as viewed from Earth. This value varies very slowly as the orbit of the Earth evolves over time in response to various internal and external influences, such as uneven mass distribution, tidal and gravitational perturbations of the sun, moon and other bodies, etc.
This is one of the fundamental values we need to know when computing the apparent position of a planet as viewed from the Earth at any given moment as it defines the instantaneous inclination of the Earth's orbit.
The ecliptic obliquity can also be used to determine the latitudes of the arctic and antarctic circles, however these values can vary slightly depending on the computational methods, the values of the applied constants, time scale, coordinates system, the applied geoid model, the accuracy of the applied nutational theory, among other factors, some of which are unpredictable.
In the computation of the arctic/antarctic circles, the difference between applying the IAU 1980 nutation series or the 2000B series only amounts to a matter of inches difference on the ground. Due to the margin of error involved in such computations and the degree to which these margins overlap, this small difference is generally too insignificant to matter when computing the latitudes of the arctic/antarctic circles.
Laskar's formula for the mean obliquity theoretically spans 10,000 years, however, I have yet to find any reliable information as to the full validity span of either of the nutational series, so how accurately the computed nutations would apply to the mean obliquity 4000 years ago or in the future from now is still a bit hazy.
Over a period of several years, these values have varied as measurement-technologies improved their accuracy and consistency. They will continue to vary for the same reasons in the future, so the same predictions based on them will also vary to a small degree from generation to generation.

Arctic Circle Map - Wikimedia Commons
As for the theoretical accuracy, below are some excerpts taken from the original paper summary:
Using the methods of the general theory given in (Laskar, 1985), we have analytically computed the differential system giving the secular variations of the orbital elements for the 8 major planets, at the order 2 with respect to the masses and up to degree 5 in the eccentricity-inclination variables with a relative precision of 10E-6. Relativistic and lunar perturbations are included. The entire system is integrated numerically over 10,000 years and then developed in Taylor expansion around J2000. We obtain new polynomial secular terms for the inner planets up to the power 10 of the time. Comparisons are made with Bretagon's theory VSOP82 and with the numerically integrated JPL ephemeris, DE102 (Newhall et al., 1983). The global accuracy is approximately 0.04202" / 1,000 yr for the inclination of the Earth. Using the theory of the rotation of the rigid Earth of Kinoshita (1977), we derive new formulas for the precessional quantities, up to the 10th power of t, and valid over 10,000 years. .....

Antarctic Circle Map - Wikimedia Commons
- Ref: http://en.wikipedia.org/wiki/Ecliptic
The algorithm used in the above program is based on data published by J. Laskar in Astronomy and Astrophysics, Vol 157, p68 (1986), New Formulas for the Precession, Valid Over 10000 years, Table 8.

Provided by the NASA Astrophysics Data System
-
J. Laskar's Formula For The Mean Obliquity
In this case, the time variable (t) of Table 8 is reckoned in terms of decamillennia (10,000 Julian years) from J2000.0 corresponding to the JD for any given moment and may be found from:

The value 84381.448 seconds of arc equates to 23° 26' 21.448" which is the mean obliquity for the ecliptic of J2000.0 TT, where:
J2000.0 = 2000-Jan-01-Sat at 12:00:00 TT
-
Based on the Table 8 data above (NGT column), the
mean obliquity (in arc seconds) of the ecliptic at time (t) is:

This value of the obliquity (ε) is the mean value. For the true, apparent obliquity of the date, a small correction for the nutation in obliquity may be applied, but is not critical. The mean value is usually sufficient for long-term trend analysis.
Jay Tanner - 2025